Type-level Programming
in Scala

Rockets explode

Types can help

Literal types

Type inhabited by a single constant value known at compile-time:

val x: 3 = 3
val y: false = false
val z: "monday" = "monday"

See SIP-23 - literal-based singleton types.

Path-dependent types

Type inhabited by a single non-necessary-constant term:

val a: Int = ???
val b: Int = ???
val c: a.type = a
val d: Int = a    // Ok because (a: Int) <: Int

val e: a.type = b // Error: found (b: Int)
                  // but required (a: Int)

It is called path-dependent because it can refer to nested members as well:

object Foo:
    val x: 3 = 3
summon[Foo.x.type =:= 3]

Dependent parameters

Singletons are used to model equality between terms.

def same(a: Any, b: a.type) = ???
same(3, 3) // Ok
same(3, 4) // Error

def same2[T](a: T, b: T) = ???
same2(3, 4) // Ok; T is inferred to be Int

Dependent return types

def id(x: Any): x.type = x

Refinement types

class Vec:
  val size: Int

val v: Vec {val size: 2} = new Vec:
  val size: 2 = 2

val vSize: 2 = v.size

Compile-time operations

Simple bounded type aliases:

infix type +[X <: Int, Y <: Int] <: Int

import scala.compiletime.ops.int.+

val a: 2 + 2 = 4

Match types

type IsEmpty[S <: String] <: Boolean = S match {
  case "" => true
  case _ => false
}

summon[IsEmpty[""] =:= true]
summon[IsEmpty["hello"] =:= false]

See Blanvillain, O., Brachthäuser, J., Kjaer, M., & Odersky, M. (2021). Type-Level Programming with Match Types. 70.

Motivation

Demonstrate a form of dependent typing. In this example, compute the type of a parameter depending on a previous argument.

Goal

printf("%s is %d")("Ada", 36) // works
printf("%s is %d")(36, "Ada") // fails

def printf(s: String)(t: ???): Unit = ()

Trick: use parameter untupling

New in Scala 3. Automatically wraps function value with n > 1 parameters in a function type of the form ((T_1, ..., T_n)) => U

def g(f: ((Int, Int)) => Unit) = ()
g({ case (x, y) => () })
g((x, y) => ()) // parameter untupling

def g2(x: (Int, Int)) = ()
g2((1, 2))
g2(1, 2)

Signature of printf

type ArgTypes[S <: String] <: Tuple = ???
def printf(s: String)(t: ArgTypes[s.type]): Unit = ()

Code

//> using scala "3.2.0"
//> using options "-Xprint:typer"
import scala.compiletime.ops.int.{+}
import scala.compiletime.ops.string.{CharAt, Length, Substring}
import scala.Tuple._

type ArgTypes[S <: String] <: Tuple = S match
  case "" => EmptyTuple
  case _ =>
    CharAt[S, 0] match
      case '%' =>
        CharAt[S, 1] match
          case 'd' => Int *: ArgTypes[Substring[S, 2, Length[S]]]
          case 's' => String *: ArgTypes[Substring[S, 2, Length[S]]]
      case _ => ArgTypes[Substring[S, 1, Length[S]]]

def printf(s: String)(t: ArgTypes[s.type]): Unit = ()

def test() =
  printf("%s is %d")("Ada", 36) // works
  summon[ArgTypes["%s is %d"] =:= (String, Int)]
  // printf("%s is %d")(36, "Ada") // fails

Related: regsafe

import regsafe.Regex

val date = Regex("""(\d{4})-(\d{2})-(\d{2})""")
"2004-01-20" match
  case date(y, m, d) =>
    s"$y was a good year for PLs."

See github.com/OlivierBlanvillain/regsafe and Blanvillain, O. (2022). Type-Safe Regular Expressions.

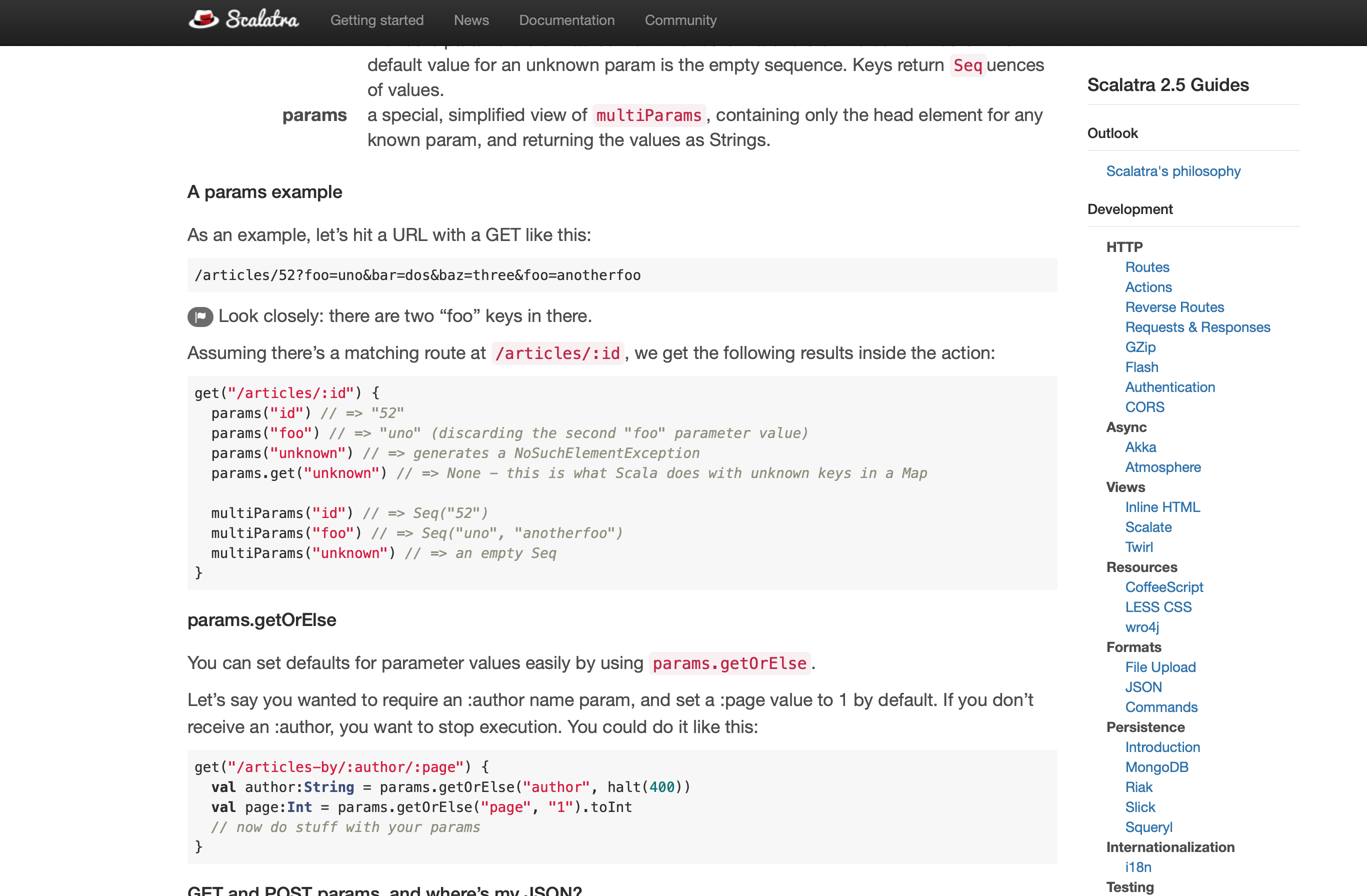
Inspiration: Scalatra

Goal

Route("user" **: stringValue **: "post" **: intValue **: EmptyTuple)
    ((userName, postId) => println(userName))

StringConverter

We present parsers from strings to arbitrary types using a StringConverter class:

class StringConverter[T](a: (x: String) => T):
  val convert = a

Trick: precise tuples

By default, type parameters of tuples are widened:

val t (Int, Int, Int) = (1, 2, 3)

As a workaround, we define our own precise tuple constructor:

extension (a: Any) infix def **:(b: Tuple): a.type *: b.type = a *: b

Code

//> using scala "3.nightly"
//> using options "-Xprint:typer"

import scala.Tuple._

def test() =
  Route("user" **: stringValue **: "post" **: intValue **: EmptyTuple)(
    (userName, postId) => println(userName)
  )

case class Route(partDefs: Tuple)(f: RouteArgTypes[partDefs.type] => Unit)

extension (a: Any) infix def **:(b: Tuple): a.type *: b.type = a *: b

class StringConverter[T](a: (x: String) => T):
  val convert = a

val intValue = StringConverter(x => x.toInt)
type IntValue = intValue.type

val stringValue = StringConverter(x => x)
type StringValue = stringValue.type

type RouteArgTypes[R <: Tuple] <: Tuple = R match
  case EmptyTuple => EmptyTuple
  case h *: t =>
    h match
      case StringConverter[r] =>
        r *: RouteArgTypes[t]
      case String =>
        RouteArgTypes[t]

@main def test2() =
  val matched: (String, Int) = matchRoute(
    List("user", "ada", "post", "42"),
    "ada" **: stringValue **: "post" **: intValue **: EmptyTuple
  )
  println(matched)

def matchRoute[R <: Tuple](parts: List[String], partDefs: R): RouteArgTypes[R] =
  partDefs match
    case _: EmptyTuple => EmptyTuple
    case t: (_ *: _) =>
      t.head match
        case c: StringConverter[_] =>
          c.convert(parts.head) *: matchRoute(parts.tail, t.tail)
        case _: String =>
          matchRoute(parts.tail, t.tail)

Motivation

For this talk: demonstrate arithmetic type-level operations.

In general, applications to:

• verification of algorithms on lists and tree,
• strong typing for machine learning tensors.

Goal

Keep track of the size of a list in its type.

Code (class and type params)

//> using scala "3.2.0"
//> using options "-Xprint:typer"

import scala.compiletime.ops.int.*

class Vec[Len <: Int, +T]:
  def ::[S >: T](x: S): Vec[Len + 1, T] = ???
  def tail: Vec[Len - 1, T] = ???
  def drop[N <: Int & Singleton](n: N): Vec[Len - N, T] = ???
  def head: T = ???
  def zip[S](that: Vec[Len, S]): Vec[Len, (T, S)] = ???
  def concat[S >: T, ThatLen <: Int](
      that: Vec[ThatLen, S]
  ): Vec[Len + ThatLen, S] = ???

def test() =
  val a = Vec[4, String]()
  val b = Vec[2, String]()
  val c = Vec[5, Int]()
  val d = a.concat(b).zip(42 :: c)
  val e = a.concat(b).zip(42 :: c)
  val f = a.drop(2).concat(b).zip(c.tail)

Current shortcomings

Cannot reason about operations with non-constant operands.

//> using scala "3.2.0"
//> using options "-Xprint:typer"
//> using file "3_vec_params_simple.scala"

def test2() =
  val size: Int = ???
  val v = Vec[size.type, Int]()
  v.zip(42 :: v.tail)
  // Error:
  //   Found: Vec[(size : Int) - (1 : Int) + (1 : Int), Int]
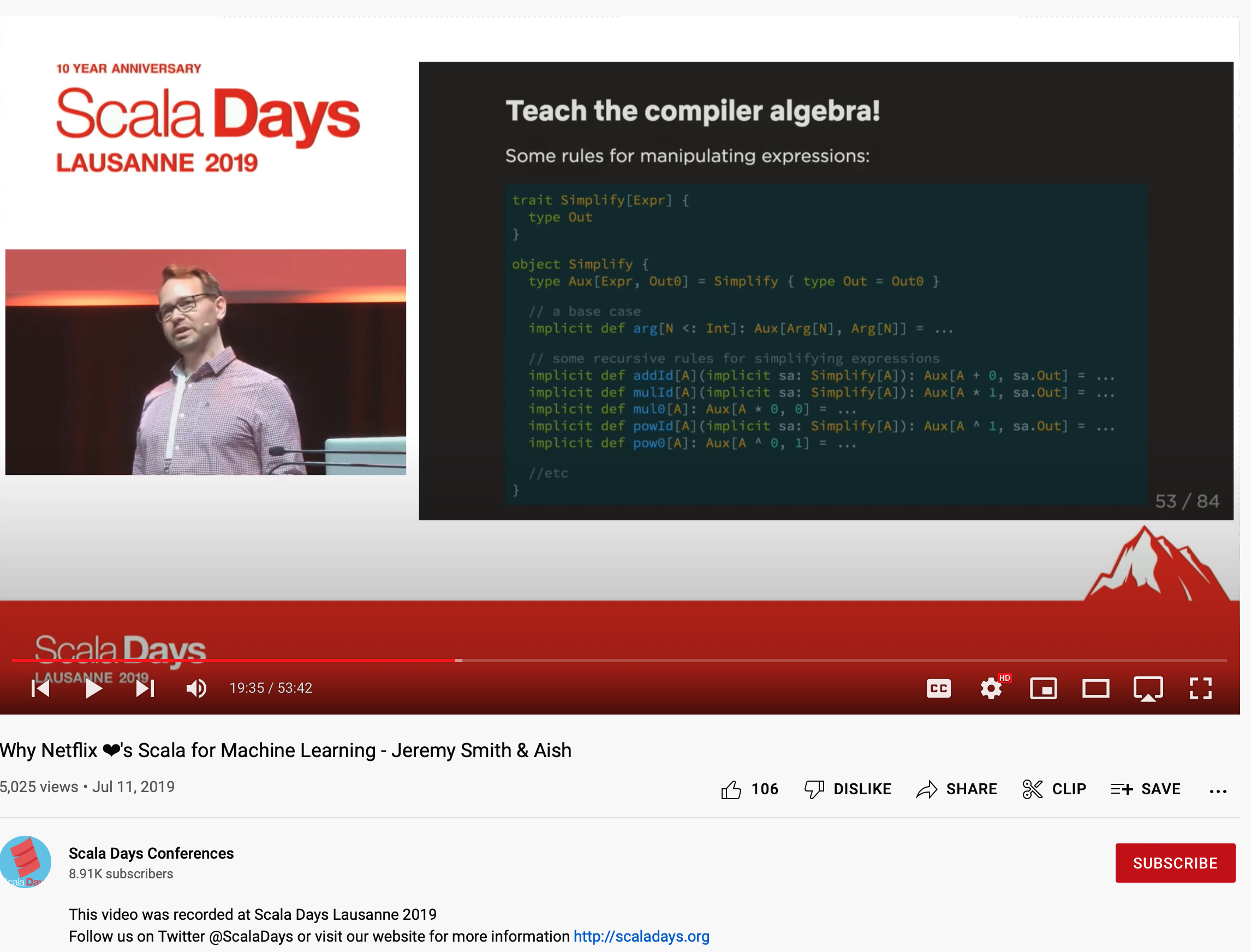
  //   Required: Vec[(size : Int), Any]

Related: Why Netflix ❤’s Scala for Machine Learning

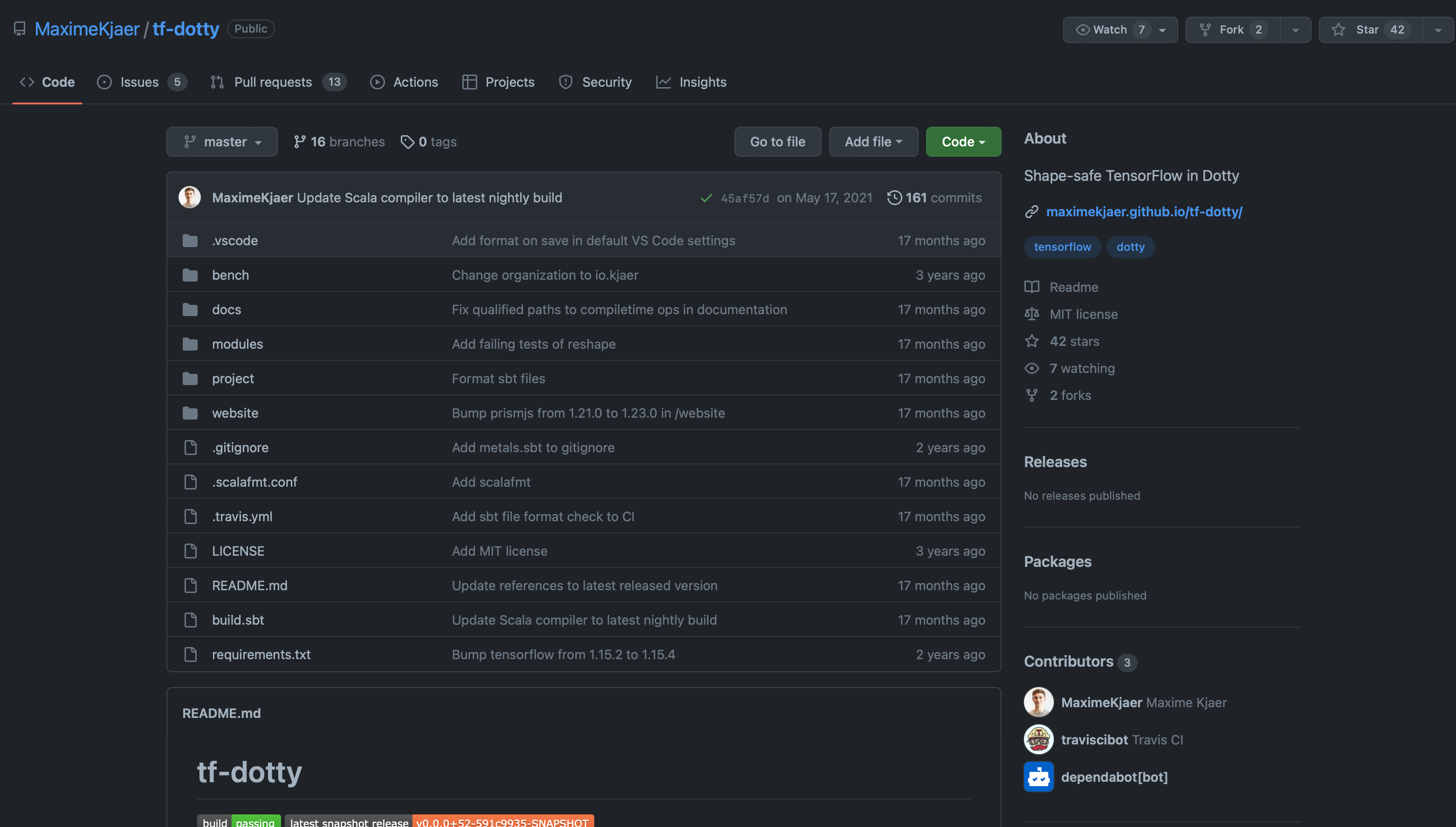
Related: tf-dotty

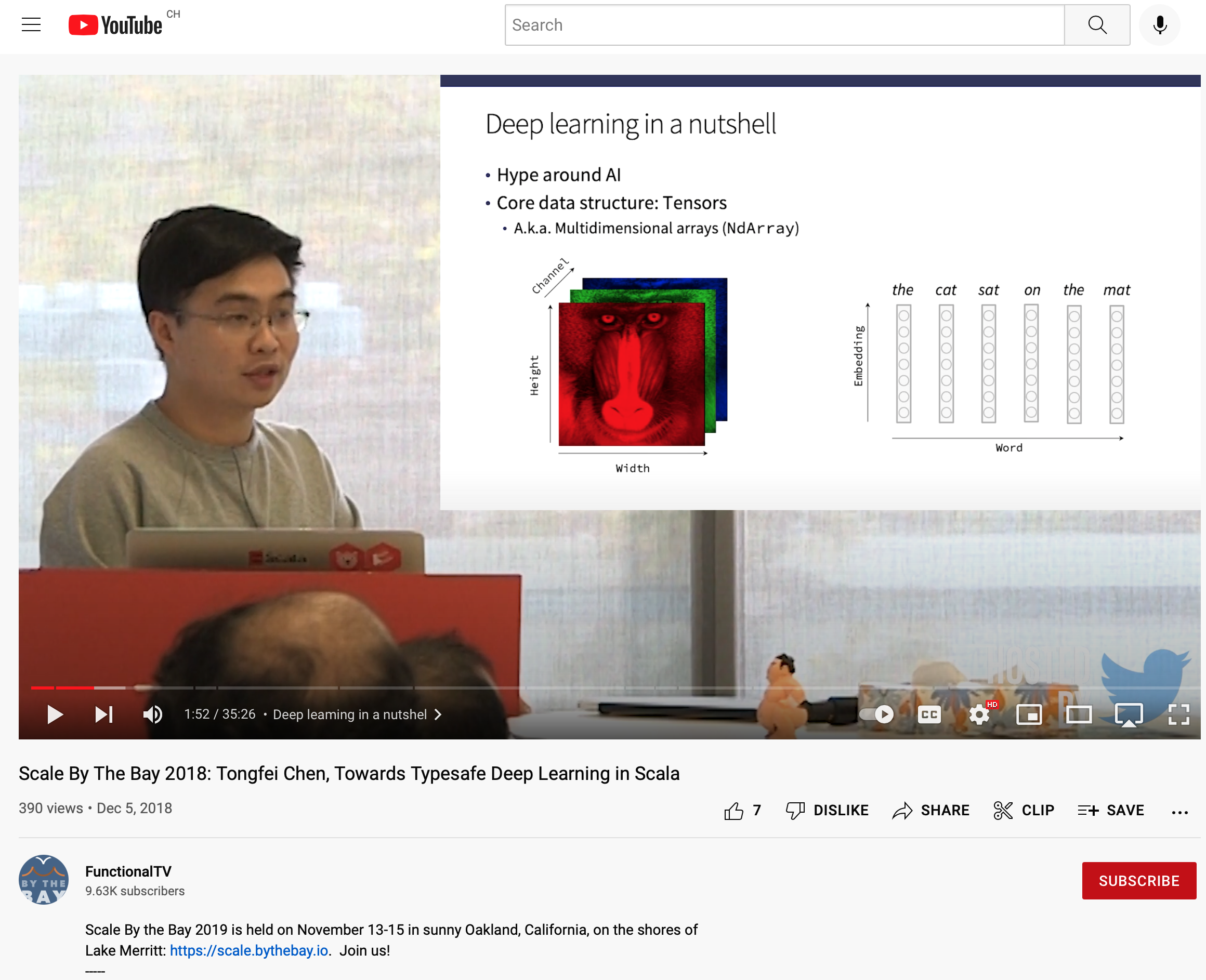
Related: Towards Typesafe Deep Learning in Scala

Ordering

// Summing x n times is normalized to x * n.
summon[n.type + m.type =:= m.type + n.type]

Grouping

// Summing x n times is normalized to x * n.
summon[2L * m.type =:= m.type + m.type]
summon[2L * m.type + 2L * m.type =:= m.type + 3L * m.type]
summon[2L * m.type * m.type =:= m.type * 2L * m.type]

Distribution

// Addition is distributed over multiplication.
summon[2L * (m.type + n.type)
       =:= 2L * m.type + 2L * n.type]

In the end, we decided not to implement distribution, because it might generate exponentially large types.

When to normalize?

Eagerly, or only when comparing types?

Should the user see normalized types?

val m: 3 = 3
val n: Int  = ???
val v /*:Vec[n.type + 3, String]*/ = Vec[m.type + n.type, String]()

Example: tf-dotty (with abstract dimensions)

val x: Int = 2
val y: Int = 2
val tensor = tf.zeros(x #: y #: SNil)
val res = tf.reshape(tensor, y #: x #: SNil)

See github.com/MaximeKjaer/tf-dotty, in particular the implementation of reshape.

See Blanvillain, O., Brachthäuser, J., Kjaer, M., & Odersky, M. (2021). Type-Level Programming with Match Types. 70.

Main ideas behind tf-dotty:

//> using scala "3.2.0"

// Inspired by https://github.com/MaximeKjaer/tf-dotty

import scala.compiletime.ops.int.*

sealed trait Shape
infix case class #:[H <: Int & Singleton, T <: Shape](h: H, t: T) extends Shape
object Nil extends Shape
type Nil = Nil.type

def mult[X <: Int, Y <: Int](x: X, y: Y) = (x * y).asInstanceOf[X * Y]

type Size[X <: Shape] <: Int = X match
  case Nil            => 1
  case #:[head, tail] => head * Size[tail]

def size[S <: Shape](s: S): Size[S] = s match
  case _: Nil               => 1
  case cons: #:[head, tail] => mult(cons.h, size(cons.t))

type Reduce[S <: Shape, Axes <: Shape] = ReduceLoop[S, Axes, 0]

type ReduceLoop[S <: Shape, Axes <: Shape, I <: Int] <: Shape = S match
  case Nil => Nil
  case #:[head, tail] =>
    Contains[Axes, I] match
      case true  => ReduceLoop[tail, Axes, I + 1]
      case false => #:[head, ReduceLoop[tail, Axes, I + 1]]

type Contains[S <: Shape, N] = S match
  case Nil            => false
  case #:[N, tail]    => true
  case #:[head, tail] => Contains[tail, N]

class Tensor[T, S <: Shape]():
  def add(t: Tensor[T, S]) = this
  def mean[A <: Shape](axes: A): Tensor[T, Reduce[S, A]] =
    Tensor[T, Reduce[S, A]]()
  def reshape[T, B <: Shape](b: B)(using Size[S] =:= Size[B]): Tensor[T, B] =
    Tensor[T, B]()

@main def test() =
  val shape = #:(5, #:(6, #:(2, Nil)))
  summon[Size[shape.type] <:< 60]
  summon[Reduce[shape.type, 0 #: Nil] <:< 6 #: 2 #: Nil]
  summon[Reduce[shape.type, 0 #: 2 #: Nil] <:< 6 #: Nil]
  summon[Reduce[shape.type, 1 #: 6 #: Nil] <:< 5 #: 2 #: Nil]

  val t1 = Tensor[Int, 5 #: 6 #: 2 #: Nil]
  val t2 = Tensor[Int, 5 #: 6 #: 2 #: Nil]
  val t3 = t1.add(t2)
  val t4 = t1.mean(#:(0, #:(2, Nil)))
  val t5 = t1.reshape(#:(2, #:(6, #:(5, Nil))))

Map method

//> using scala "3.2.0"
//> using options "-Xprint:typer"

import scala.compiletime.ops.int.*

enum Vec[Len <: Int, +T]:
  case Nil extends Vec[0, Nothing]
  case NotNil[N <: Int, T]() extends Vec[N, T]

  def ::[S >: T](x: S): Vec[Len + 1, T] = ???
  def tail: Vec[Len - 1, T] = ???
  def head: T = ???

  def map[S](f: T => S): Vec[Len, S] =
    this match
      case Vec.Nil => Vec.Nil
      case _       => f(this.head) :: this.tail.map(f)

Refinement version

class SizedList[+T](private val l: List[T]):
  val size = l.size

  def ::[S >: T](x: S)
    : SizedList[S] {val size: SizedList.this.size.type + 1} = ???
  def tail: SizedList[T] {val size: SizedList.this.size.type - 1} = ???
  def head: T = ???

val SizedNil = new SizedList(Nil):
  override val size: 0 = 0

@main def test =
  val xs: SizedList{val size: 2} = "a" :: "b" :: SizedNil

Map with refinement

Wrong attempt:

def mapWrong[S](f: T => S): SizedList[S] { val size: SizedList.this.size.type } =
    if size == 0 then SizedNil
    else f(this.head) :: this.tail.map(f)

Helper method to type Nil

private def nilOr[T](
    f: => T
): SizedList[Nothing] { val size: 0 & SizedList.this.size.type } | T =
  if size == 0 then asInstanceOf
  else f

Code (refinement version)

//> using scala "3.2.0"
//> using options "-Xprint:typer"

import scala.compiletime.ops.int.*

class Vec[+T](private val l: List[T]):
  val size = l.size

  def ::[S >: T](x: S): Vec[S] { val size: SizedList.this.size.type + 1 } = ???
  def tail: Vec[T] { val size: SizedList.this.size.type - 1 } = ???
  def head: T = ???
  def map[S](f: T => S): Vec[S] { val size: SizedList.this.size.type } =
    nilOr(f(this.head) :: this.tail.map(f))

  def zip[S](
      that: Vec[S] { val size: SizedList.this.size.type }
  ): Vec[(T, S)] { val size: SizedList.this.size.type } =
    nilOr((this.head, that.head) :: this.tail.zip(that.tail))

  // Manual GDAT-like reasoning
  private def nilOr[T](
      f: => T
  ): Vec[Nothing] { val size: 0 & SizedList.this.size.type } | T =
    if size == 0 then asInstanceOf
    else f

val SizedNil = new SizedList(Nil):
  override val size: 0 = 0

/*object SizedNil:
  def unapply[T](l: SizedList[T]): Option[SizedList[Nothing] {val size: 0 & l.size.type}] =
    if l.size == 0 then Some(l.asInstanceOf)
    else None*/

Why not always infer precise types?

Problem 1: usability

Problem 2: performance

Problem 3: backward compatibility

Precising types can for example break previously working implicits search.

class A
class B extends A
class Inv[X]
given inv: Inv[A] = Inv()
def f3[N](x: N)(using Inv[N]) = 1984

val b = B()

f3(b: A) // works

f3[A](b: B) // works
f3(b: B)(using inv) // works
f3(b: B) // error: no given instance of type Inv[B]

Solution 1: separate term-level constructs?

extension (a: Any) infix def **:(b: Tuple): a.type *: b.type =
  a *: b

extension (a: Int) infix def +!(b: Int): a.type + b.type =
  (a + b).asInstanceOf[a.type + b.type]

class Person(name: String)
val person: Person {name: "Ada"} =
  Person.precise("Ada")

Advantage: simple, nothing to change in the language.

Drawbacks:

• verbosity (and not only for API writers),
• hard to come up with an elegant syntax.

Solution 2: always precise and widen?

By default, singletons and unions are used to type literal, term references and conditionals, but widened during inference:

val x /*: Int*/ = 3 /*: 3*/
val y /*: Int*/ = x /*: x.type*/
val z /*: Int*/ = if c then 1 else 2 /*: 1 | 2*/

Could we do the same for constructor types, type-level operations and tuples?

val x /*: Person*/ = Person("Ada") /*: Person{val name: "Ada"}*/
val y /*: Int*/ = a + b /*: a.type + b.type*/
val z /*: (Int, Int, Int)*/ = (1, 2, 3) /*: (1,2,3)*/

Advantage:

• similar to an existing mechanism.

Drawbacks:

• verbosity (and not only for API writers),
• risky for performance.

Solution 3: type depending on the expected type

By default, the result type of a match is the LUB of the result types of the cases

val v4 /*: Boolean */ = x match
  case _: String => true
  case _ => false

type IsString[T <: Any] = T match {
  case String => true
  case _ => false }
val v5: IsString[x.type] = x match
  case _: String => true
  case _ => false

Could we do the same for constructor types, type-level operations and tuples?

Advantage:

• similar to an existing mechanism.

Drawbacks:

• verbosity (and not only for API writers),
• complex implementation.

Solution 4: a dedicated inference mode?

Proposition: type everything precisely when a value or a function is annotated with the precise keyword.

precise def precise() =
  val v1 = 1
  val v2 = 2 + v1
  precise def isString(x: Any) = x match
    case _: String => true
    case _ => false
  val v3 = isString(42)
  val v4 = Foo(42)

A separate inference mode was first proposed in “Coming to Terms with Your Choices: An Existential Take on Dependent Types” (with the dependent here). Our implementation follows a similar but weaker semantic. In our case, precise simply instructs the system to type the body of the function “as precisely as possible”, while in the linked technical report it means “as precise as its implementation”.

Inferred types:

precise def precise() =
  val v1 /*: (v1: (1: Int))*/ = 1
  val v2 /*: (v2: (3: Int))**/ = 2 + v1
  precise def isString(x: Any) /*: (x : Any) match {
    case String => (true : Boolean)
    case Any => (false : Boolean)
  }*/ = x match
    case _: String => true
    case _ => false
  val v3 /*: (false: Boolean) */ = isString(42)
  val v4 /*: Foo {val x = 42} */ = Foo(42)

Advantage:

• finally less verbose 😻

Drawback:

• brings more complexity to the language.

How should precise inference propagate?

precise def id(x: Int): x.type = x
val n: Int = ???
val y = id(n + 3)