Logically Qualified Types
for Scala 3

Introduction

I am Matt Bovel (@mbovel).

Motivating example: Safe list zip

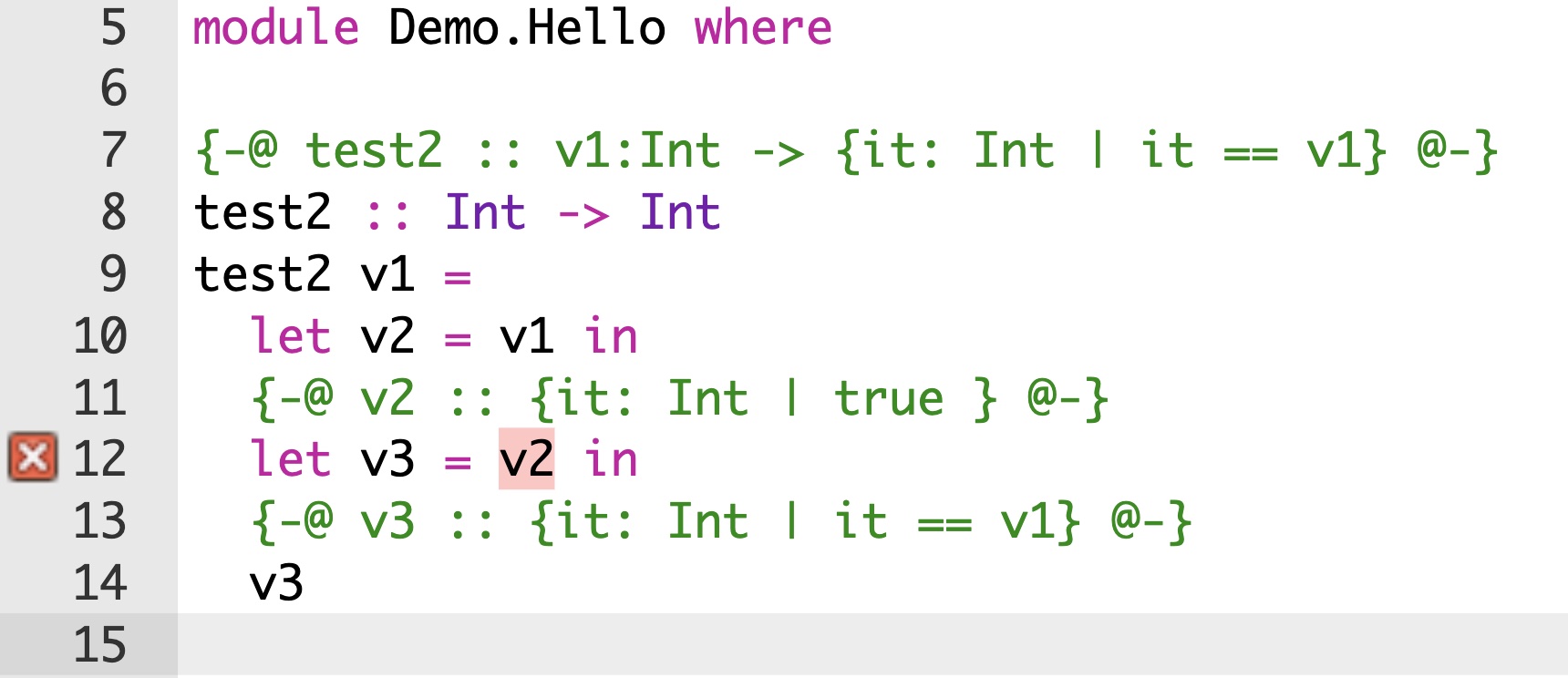
Consider the standard zip function:

def zip[A, B](
  as: List[A],
  bs: List[B]
): List[(A, B)] =
  ...

Specify using assertions 😕

def zip[A, B](
  as: List[A],
  bs: List[B]
) : List[(A, B)] = {
  require(as.size == bs.size)
  ...
}.ensure(_.size == as.size)

Specify using dependent types 😕

def zip[A, B](
  as: List[A],
  bs: List[B] {
    val size: as.size.type
  }
): List[(A, B)] {
  val size: as.size.type
} = ...

Specify using logically qualified types ! 🤩

Introducing logically qualified types:

def zip[A, B](
  as: List[A],
  bs: List[B] with bs.size == as.size
): {l: List[(A, B)] with l.size == as.size} = ...

In other languages

Main difference with Liquid Haskell

Liquid Haskell is a plugin that runs after type checking.

Syntax

type NonEmptyList[A] = { l: List[A] with l.nonEmpty }

• l: binder
• List[A]: parent type
• l.nonEmpty: qualifier (predicate)

case class Box(value: Any)
type IntBox = Box { val value: Int }

Shorthand syntax

When a binder already exists, such as in:

def zip[A, B](as: List[A], bs: {bs: List[B] with bs.size == as.size})

def zip[A, B](as: List[A], bs: List[B] with bs.size == as.size)

More list API examples 🥳

def zip[A, B](as: List[A], bs: List[B] with bs.size == as.size):
  {l: List[(A, B)] with l.size == as.size}

def concat[T](as: List[T], bs: List[T]):
  {rs: List[T] with rs.size == as.size + bs.size}

val xs: List[Int] = ...
val ys: List[Int] = ...
zip(concat(xs, ys), concat(ys, xs))
zip(concat(xs, ys), concat(xs, xs)) // error

What are valid predicates?

var x = 3
val y: Int with y == 3 = x // ⛔️ x is mutable

class Box(val value: Int)
val b: Box with b == Box(3) = Box(3) // ⛔️ Box has equality by reference

How to introduce qualified types?

For backward compatibility and performance reasons, qualified types are not inferred from terms by default. The wider type is inferred instead:

val x: Int = readInt()
val y /* : Int */ = x + 1

Selfification

However, when a qualified type is expected, the compiler attempts to selfify the typed expression: that is, to give e: T the qualified type x: T with x == e:

val x: Int = readInt()
val y: Int with (y == x + 1) = x + 1

def f(i: Int): Int = i * 2
val z: Int with (z == x + f(x)) = x + f(x)

Runtime checks

When static checking fails, a qualified type can be checked at runtime using pattern matching:

val idRegex = "^[a-zA-Z_][a-zA-Z0-9_]*$"
type ID = {s: String with s.matches(idRegex)}

"a2e7-e89b" match
    case id: ID => // matched: `id` matches idRegex
    case id     => // didn't match

Runtime checks: .runtimeChecked

You can also use .runtimeChecked (SIP-57) when the check must always pass:

val id: ID = "a2e7-e89b".runtimeChecked

val id: ID =
  if ("a2e7-e89b".matches(idRegex)) "a2e7-e89b".asInstanceOf[ID]
  else throw new IllegalArgumentException()

Runtime checks: List.collect

Scala type parameters are erased at runtime, so we cannot match on a List[T].

type Pos = { v: Int with v >= 0 }

val xs = List(-1,2,-2,1)
xs.collect { case x: Pos => x } : List[Pos]

Subtyping

How does the compiler check {x: T with p(x)} <: {y: S with q(y)}?

1. Check T <: S
2. Check p(x) implies q(x) for all x

Subtyping: constant folding

{v: Int with v == 1 + 1}     <: {v: Int with v == 2}

Subtyping: normalization

Arithmetic expressions are normalized using standard algebraic properties, for example commutativity of addition:

{v: Int with v == x + 1}     <: {v: Int with v == 1 + x}

{v: Int with v == y + x}     <: {v: Int with v == x + y}

{v: Int with v == x + 3 * y} <: {v: Int with v == 2 * y + (x + y)}

Subtyping: unfolding

Remember: qualified types are not inferred from terms by default. However, the solver can unfold definitions of local val (only), even when they have an imprecise type:

val x: Int = ...
val y: Int = x + 1

{v: Int with v == y} =:= {v: Int with v == x + 1}

Subtyping: equality reasoning

Transitivity of equality:

{v: Int with v == a && a == b} <: {v: Int with v == b}

{v: Int with a == b}           <: {v: Int with f(a) == f(b)}

Subtyping with other Scala types

Singleton qualified types are subtypes of literal types:

{v: Int with v == 3} <: 3

Future work: SIP

Some work remains on UX (error messages, IDE support, documentation).

Future work: term-parameterized types

extension [T](list: List[T])
  def get(index: Int with index >= 0 && index < list.size): T = ...

type Range(from: Int, to: Int) = {v: Int with v >= from && v < to}
extension [T](list: List[T])
  def get(index: Range(0, list.size)): T = ...

Future work: flow-sensitive typing

Works with pattern matching:

x match
  case x: Int with x > 0 =>
    x: {v: Int with v > 0}

if x > 0 then
  x: {v: Int with v > 0}

Future work: flow-sensitive typing

Crucially, this would be required for “GADT-like” reasoning with qualified types:

enum MyList[+T]:
  case Cons(head: T, tail: MyList[T])
  case Nil

def myLength(xs: MyList[Int]): Int =
  xs match
    case MyList.Nil =>
      // Add assumption xs == MyList.Nil
      0
    case MyList.Cons(_, xs1) =>
      // Add assumption xs == MyList.Cons(?, xs1)
      1 + myLength(xs1)

Future work: integration with SMT solvers

Our solver is lightweight 👍 but incomplete 👎.

{v: Int with v > 2} <: {v: Int with v > 0}

Conclusion

• Syntax: {x: T with p(x)},
• Selfification: e: T becomes x: T with x == e when needed,
• Runtime checks: pattern matching and .runtimeChecked,
• Subtyping: custom lightweight solver,
• Future work: SIP, term-parameterized types, flow-sensitive typing, SMT integration.

---

• Two-page summary
• Prototype (dotty#21586)

Backup/outdated slides

Bonus: works with implicit resolution

type Pos = { v: Int with v >= 0 }
type Neg = { v: Int with v < 0 }

trait Show[-A]:
  def apply(a: A): String
given show1: Show[Pos] with
  def apply(a: Pos): String = "I am a positive integer!"
given show2: Show[Neg] with
  def apply(a: Neg): String = "I am a negative integer!"
def show[A](a: A)(using s: Show[A]): String = s.apply(a)

def f(x: Int with x == 42, y: Int with y == -42): Unit =
  println(show(x)) // I am a positive integer!
  println(show(y)) // I am a negative integer!

Checking integer equality at the type level

def checkSame(dimA: Int, dimB: dimA.type): Unit = ()
checkSame(3, 3) // ok
checkSame(3, 4) // error

Checking integer equality at the type level 🥲

def checkSame(dimA: Int, dimB: dimA.type): Unit = ()
val x = 3
val y = 3
checkSame(x, y) // error

Checking integer equality at the type level 😄

def checkSame(dimA: Int, dimB: dimA.type): Unit = ()
val x: 3 = 3
val y: 3 = 3
checkSame(x, y) // ok

Checking integer equality at the type level 😢

def checkSame(dimA: Int, dimB: dimA.type): Unit = ()
def readInt(): Int = ...
val x: Int = readInt()
val y = x
val z = y
checkSame(y, z) // error

Checking integer equality at the type level 😁

def checkSame(dimA: Int, dimB: dimA.type): Unit = ()
val x: Int = readInt()
val y: x.type = x
val z: x.type = x
checkSame(y, z) // okay

Checking integer equality at the type level 😓

def checkSame(dimA: Int, dimB: dimA.type): Unit = ()
val x: Int = readInt()
val y: Int = readInt()
val z = x + y
val a = y + x
checkSame(z, a) // error

Checking integer equality at the type level 😲

def checkSame(dimA: Int, dimB: dimA.type): Unit = ()
import scala.compiletime.ops.int.+
val x: 3 = 3
val y: 5 = 5
val z: x.type + y.type = x + y
val a: y.type + x.type = y + x
checkSame(z, a) // error

Checking integer equality at the type level 😭

import scala.compiletime.ops.int.+
val x: Int = readInt()
val y: Int = readInt()
val z: x.type + y.type = x + y // error
val a: y.type + x.type = y + x // error
checkSame(z, a) // error